6.3. Jaccard Similarity¶
The single-source version of this problem is:
Given a specific vertex A, find other vertices B that are most similar to A.
This is done by computing a similarity metric for each vertex B and then rank-ordering the vertices by that score.
The Jaccard similarity metric is between two different vertices A and B. It is computed as the ratio of the intersection of their neighboring U vertex sets to the union of their neighbor sets. The diagram shows, for a given A and B, a neighborhood union of size 8. The intersection of the two neighborhoods include: {1, 3, 7}, so the intersection size is 3. If the intersection is the same size as the union, that means the two vertices have identical neighborhoods and are therefore considered to be most similar.
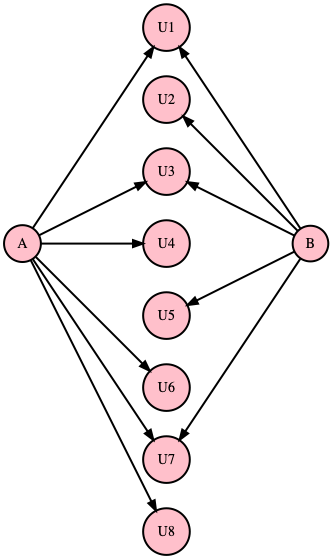
Two Vertices with Similar Neighborhoods¶
This metric is based on the graph topology and is not influenced by the vertex and edge property values. It may be more interesting to include data values as part of a Jaccard analysis.
The overall flow of this analysis using xGT involves these phases:
Build a connectivity graph to drastically reduce the search space
Find all two-paths from A to B through intermediate vertices Ux over the connectivity graph
Group all of the two-paths by the B vertex to get a count of the number of two paths from A to B (which is the size of the intersection)
Use the outdegree of B within the connectivity graph to compute the size of the union, which leads to the similarity metric
6.3.1. Connect to the xGT Server¶
Before embarking on phase 1, some prelimiaries are required to interact
with the xGT server.
import xgt
import getpass
server=xgt.Connection(userid=getpass.getuser(),
credentials=getpass.getpass())
server.server_version
Password: ········
'1.4.0'
6.3.2. Retrieve Metadata about the Graph¶
Select specific parts of the graph to analyze:
A_VERTEX_KEYselects the key of the unique vertex to play the role of A. Note that this vertex is the single source and the Jaccard computation will find other vertices most similar to A.EDGE_FRAME_NAMEis the name of the edge frame connecting A to all of the B vertices.NAMESPACEis the name of the namespace holding the desired edge frame.
From the selected information, the components of the graph in the
xGT server are extracted.
A_VERTEX_KEY='VPN'
EDGE_FRAME_NAME='Netflow'
NAMESPACE='graph'
FULL_EDGE_FRAME_NAME=NAMESPACE + '__' + EDGE_FRAME_NAME
edge = server.get_edge_frame(FULL_EDGE_FRAME_NAME)
source_vertex = server.get_vertex_frame(edge.source_name)
target_vertex = server.get_vertex_frame(edge.target_name)
VERTEX_KEY = source_vertex.key
(source_vertex, edge, target_vertex, VERTEX_KEY)
(<xgt.graph.VertexFrame at 0x1093b3af0>,
<xgt.graph.EdgeFrame at 0x1093b3ee0>,
<xgt.graph.VertexFrame at 0x1093d84c0>,
'device')
6.3.3. Define Utility Functions¶
These utility functions are used during the phases to interact with the
xGT server.
#---- Utility functions for launching queries
def run_query(server, query, table_name = NAMESPACE + "__answers",
drop_answer_table=True, show_query=False):
if drop_answer_table and table_name is not None:
server.drop_frame(table_name)
if query[-1] != '\n':
query += '\n'
if table_name is not None:
query += 'INTO {}'.format(table_name)
if show_query:
print("Query:\n" + query)
job = server.schedule_job(query)
if show_query:
print("Launched job {} at time: {}".format(job.id, time.asctime()))
server.wait_for_job(job)
if table_name is None:
return None
table = server.get_table_frame(table_name)
return table
import time
def run_query_and_count(server, query, table_name = NAMESPACE + "__answers",
drop_answer_table=True, show_query=False):
server.drop_frame(table_name)
start_time = time.time()
server.wait_for_metrics()
wait_time = time.time() - start_time
if wait_time > 30:
print('Time to wait for metrics: {:3,.2f}'.format(wait_time))
table = run_query(server, query, table_name, drop_answer_table, show_query)
# Retrieve count
count = table.get_data()[0][0]
return count
# Utility to print the data sizes currently in xGT
def print_data_summary(server, frames=None):
if frames is None:
frames = server.get_table_frames() + server.get_vertex_frames() + server.get_edge_frames()
if len(frames)==0:
print("No data has been defined")
for frame in frames:
frame_name = frame.name
if isinstance(frame, xgt.EdgeFrame):
frame_type = 'edge'
elif isinstance(frame, xgt.VertexFrame):
frame_type = 'vertex'
elif isinstance(frame, xgt.TableFrame):
frame_type = 'table'
else:
frame_type = 'unknown'
print("{} ({}): {:,}".format(frame_name, frame_type, frame.num_rows))
print_data_summary(server)
graph__Devices (vertex): 157,875
graph__Netflow (edge): 222,323,503
6.3.4. Phase 1: Build a Connectivity Graph¶
Between any two vertices, a -> b, there may be many edges, perhaps
millions.
To compute Jaccard similarity, all we need to know is if there is at least one or if there are zero edges.
We superimpose a connectivity graph on the same vertex set and leave either zero or one edges between every pair of vertices.
This phase consists of finding distinct vertex pairs with at least one edge. Note that this results in a table with the source and target vertex keys. From there we populate a new edge frame.
# create connectivity edge
server.drop_frame(NAMESPACE + '__ConnectedTo')
edge_schema = dict(edge.schema)
connected_to = server.create_edge_frame(
name=NAMESPACE + '__ConnectedTo',
schema=[[edge.source_key, edge_schema[edge.source_key]],
[edge.target_key, edge_schema[edge.target_key]]],
source=edge.source_name,
target=edge.target_name,
source_key=edge.source_key,
target_key=edge.target_key)
connected_to
<xgt.graph.EdgeFrame at 0x1093b3a90>
%%time
# Find distinct pairs of vertices over edge frame
q = """
MATCH (a)-[e1:{edge_frame}]->(b)
WHERE unique_vertices(a, b)
RETURN DISTINCT a.{vertex_key} AS a, b.{vertex_key} AS b
""".format(edge_frame=FULL_EDGE_FRAME_NAME, vertex_key=VERTEX_KEY)
table = run_query(server, q, table_name=NAMESPACE + '__DistinctConnections', show_query=True)
print("Number of intermediate rows: {:,}".format(table.num_rows))
Query:
MATCH (a)-[e1:graph__Netflow]->(b)
WHERE unique_vertices(a, b)
RETURN DISTINCT a.device AS a, b.device AS b
INTO graph__DistinctConnections
Launched job 126 at time: Wed Jul 22 08:57:19 2020
Number of intermediate rows: 559,680
CPU times: user 7.15 ms, sys: 4.68 ms, total: 11.8 ms
Wall time: 7.7 s
%%time
# From table of distinct vertex pairs, populate connectivity edge
q = """
MATCH (ab:{distinct_connections})
MERGE (a : {source_vertex_frame_name} {{ {source_vertex_key} : ab.a }})
MERGE (b : {target_vertex_frame_name} {{ {target_vertex_key} : ab.b }})
CREATE (a)-[e: {connected_to} {{ }}]->(b)
""".format(distinct_connections=NAMESPACE + '__DistinctConnections',
source_vertex_frame_name=edge.source_name, target_vertex_frame_name=edge.target_name,
source_vertex_key=source_vertex.key, target_vertex_key=target_vertex.key,
connected_to=NAMESPACE + '__ConnectedTo')
run_query(server, q, table_name=None, show_query=True)
server.drop_frame(NAMESPACE + '__DistinctConnections')
Query:
MATCH (ab:graph__DistinctConnections)
MERGE (a : graph__Devices { device : ab.a })
MERGE (b : graph__Devices { device : ab.b })
CREATE (a)-[e: graph__ConnectedTo { }]->(b)
Launched job 176 at time: Wed Jul 22 08:57:27 2020
CPU times: user 4.76 ms, sys: 2.45 ms, total: 7.2 ms
Wall time: 218 ms
True
6.3.5. Phase 2: Count Two Paths from A to B¶
This phase finds two-paths from the A vertex to all other B vertices through an intermediate vertex U.
Since A is fixed, we retain distinct combinations of U and B, along with the sum of the outdegrees of A and B, which we use in a later phase. This outdegree sum turns out to be the same as the sum of the size of the union of A and B neighborhoods and the size of their intersection.
%%time
import pandas
q = """
MATCH (a)-[e1:{connected_to}]->(u)<-[e2:{connected_to}]-(b)
WHERE unique_vertices(a, b, u)
AND a.{vertex_key} = "{a_vertex_key}"
RETURN DISTINCT b.{vertex_key} AS b, u.{vertex_key} as u,
outdegree(a, {connected_to}) + outdegree(b, {connected_to}) AS outDegreeSum
""".format(connected_to=NAMESPACE + '__ConnectedTo',
vertex_key=source_vertex.key, a_vertex_key=A_VERTEX_KEY)
table = run_query(server, q, table_name=NAMESPACE + '__phase2', show_query=True)
print("Number of intermediate rows: {:,}".format(table.num_rows))
if table.num_rows > 100:
print("Showing the first 100 rows:")
df=table.get_data_pandas(0, 100)
else:
df=table.get_data_pandas()
df
Query:
MATCH (a)-[e1:graph__ConnectedTo]->(u)<-[e2:graph__ConnectedTo]-(b)
WHERE unique_vertices(a, b, u)
AND a.device = "VPN"
RETURN DISTINCT b.device AS b, u.device as u,
outdegree(a, graph__ConnectedTo) + outdegree(b, graph__ConnectedTo) AS outDegreeSum
INTO graph__phase2
Launched job 190 at time: Wed Jul 22 08:57:29 2020
Number of intermediate rows: 256,417
Showing the first 100 rows:
CPU times: user 420 ms, sys: 139 ms, total: 559 ms
Wall time: 2.07 s
| b | u | outDegreeSum | |
|---|---|---|---|
| 0 | Comp853122 | Comp072974 | 614 |
| 1 | Comp217088 | Comp008822 | 620 |
| 2 | Comp077180 | Comp857132 | 605 |
| 3 | Comp873655 | Comp908480 | 613 |
| 4 | Comp064818 | Comp184712 | 605 |
| ... | ... | ... | ... |
| 95 | Comp356840 | Comp604291 | 628 |
| 96 | Comp281329 | Comp275646 | 605 |
| 97 | Comp639272 | Comp037853 | 595 |
| 98 | Comp970485 | Comp398468 | 612 |
| 99 | Comp817584 | Comp275646 | 624 |
100 rows × 3 columns
6.3.6. Phase 3: Group By B and Count Number of U Vertices¶
The count of distinct U vertices for A -> U <- B represents the
size of the intersection of the neighborhoods of A and B.
We also carry forward the sum of the outdegree of A and B to the next phase.
%%time
q = """
MATCH (row:{phase2})
RETURN row.b AS b, row.outDegreeSum AS outDegreeSum,
COUNT(*) AS intersectionSize
""".format(phase2=NAMESPACE + '__phase2')
table = run_query(server, q, table_name=NAMESPACE + '__phase3')
server.drop_frame(NAMESPACE + '__phase2')
df = table.get_data_pandas()
df
CPU times: user 80.9 ms, sys: 9.06 ms, total: 90 ms
Wall time: 474 ms
| b | outDegreeSum | intersectionSize | |
|---|---|---|---|
| 0 | Comp576990 | 591 | 12 |
| 1 | Comp250033 | 597 | 13 |
| 2 | Comp125251 | 589 | 10 |
| 3 | Comp753523 | 607 | 28 |
| 4 | Comp528543 | 580 | 1 |
| ... | ... | ... | ... |
| 24615 | Comp704389 | 595 | 15 |
| 24616 | Comp505509 | 603 | 23 |
| 24617 | Comp181012 | 585 | 4 |
| 24618 | Comp747115 | 619 | 30 |
| 24619 | IP479316 | 585 | 2 |
24620 rows × 3 columns
6.3.7. Phase 4: Compute Jaccard Score¶
We now scan the latest intermediate table and compute the Jaccard score from the counts computed in previous phases.
%%time
q = """
MATCH (row:{phase3})
RETURN row.b AS b, row.intersectionSize AS intersectionSize,
row.outDegreeSum - row.intersectionSize AS union_size,
(row.intersectionSize + 0.0) / (row.outDegreeSum - row.intersectionSize) AS jaccard_score
ORDER BY jaccard_score DESC
LIMIT 50
""".format(phase3=NAMESPACE + '__phase3')
table = run_query(server, q, table_name=NAMESPACE + '__jaccard')
server.drop_frame(NAMESPACE + '__phase3')
df = table.get_data_pandas()
df
CPU times: user 7.46 ms, sys: 2.78 ms, total: 10.2 ms
Wall time: 147 ms
| b | intersectionSize | union_size | jaccard_score | |
|---|---|---|---|---|
| 0 | Comp678443 | 87 | 665 | 0.130827 |
| 1 | Comp030334 | 74 | 781 | 0.094750 |
| 2 | Comp965575 | 72 | 780 | 0.092308 |
| 3 | Comp257274 | 72 | 782 | 0.092072 |
| 4 | Comp866402 | 72 | 783 | 0.091954 |
| 5 | Comp211931 | 50 | 580 | 0.086207 |
| 6 | Comp769797 | 50 | 584 | 0.085616 |
| 7 | Comp148004 | 54 | 637 | 0.084772 |
| 8 | Comp148684 | 49 | 580 | 0.084483 |
| 9 | Comp464369 | 49 | 583 | 0.084048 |
| 10 | Comp889106 | 50 | 598 | 0.083612 |
| 11 | Comp501848 | 48 | 586 | 0.081911 |
| 12 | Comp415532 | 48 | 586 | 0.081911 |
| 13 | Comp725432 | 48 | 592 | 0.081081 |
| 14 | Comp468329 | 47 | 583 | 0.080617 |
| 15 | Comp304006 | 47 | 583 | 0.080617 |
| 16 | Comp055001 | 47 | 585 | 0.080342 |
| 17 | Comp211432 | 46 | 582 | 0.079038 |
| 18 | Comp377866 | 46 | 584 | 0.078767 |
| 19 | Comp507194 | 46 | 584 | 0.078767 |
| 20 | Comp613192 | 46 | 585 | 0.078632 |
| 21 | Comp771132 | 46 | 586 | 0.078498 |
| 22 | Comp599337 | 46 | 587 | 0.078365 |
| 23 | Comp719990 | 45 | 582 | 0.077320 |
| 24 | Comp643534 | 46 | 595 | 0.077311 |
| 25 | Comp881722 | 45 | 583 | 0.077187 |
| 26 | Comp493395 | 45 | 583 | 0.077187 |
| 27 | Comp614801 | 45 | 585 | 0.076923 |
| 28 | Comp764436 | 45 | 586 | 0.076792 |
| 29 | Comp302339 | 45 | 592 | 0.076014 |
| 30 | Comp991220 | 46 | 608 | 0.075658 |
| 31 | Comp130208 | 44 | 582 | 0.075601 |
| 32 | Comp924691 | 45 | 598 | 0.075251 |
| 33 | Comp943564 | 44 | 585 | 0.075214 |
| 34 | Comp018032 | 44 | 585 | 0.075214 |
| 35 | Comp498377 | 44 | 590 | 0.074576 |
| 36 | Comp210768 | 44 | 592 | 0.074324 |
| 37 | Comp688526 | 43 | 581 | 0.074010 |
| 38 | Comp958822 | 43 | 581 | 0.074010 |
| 39 | Comp591316 | 43 | 582 | 0.073883 |
| 40 | Comp856137 | 43 | 582 | 0.073883 |
| 41 | Comp354119 | 43 | 582 | 0.073883 |
| 42 | Comp617264 | 43 | 582 | 0.073883 |
| 43 | Comp498743 | 43 | 583 | 0.073756 |
| 44 | Comp559728 | 43 | 584 | 0.073630 |
| 45 | Comp084630 | 44 | 598 | 0.073579 |
| 46 | Comp356840 | 43 | 585 | 0.073504 |
| 47 | Comp077821 | 43 | 585 | 0.073504 |
| 48 | Comp452053 | 43 | 585 | 0.073504 |
| 49 | Comp959644 | 43 | 587 | 0.073254 |